Subtraction Strategies
Strategies are listed from the earliest strategies up through the standard algorithm. Many are used side by side, but it is important to understand that the variety of strategies are used to build a deeper conceptual understanding and move to a more procedural model backed by conceptual understanding of subtraction. Keep in mind that mastery of the standard algorithm of subtraction is not expected until grade 4 per the Maine Learning Results and Common Core State Standards, however students will begin practicing the standard algorithm along side other strategies much earlier than grade 4.
Models 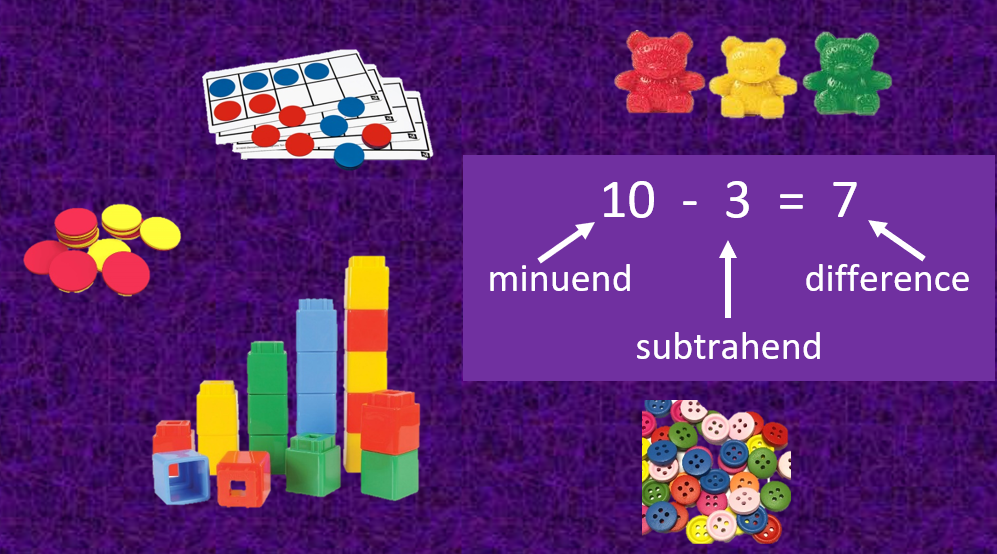
Students first experience subtraction through the use of models. They may use a variety of manipulatives such as cubes, counting bears, buttons, five and ten frames, fingers, or counters. Students may also draw representations or pictures to model the mathematics or even act out the subtraction physically. These models help students understand the action happening in the earliest subtraction problems. Models can still be helpful as students work across part-part-total, change, and comparative subtraction problems. Students also need practice finding the missing values in all locations of a subtraction problem - the minuend, subtrahend, and the difference. For more examples of subtraction problem situations, check out the Glossary Table 1 from the Common Core State Standards for Mathematics.
Counting Back (or Up)
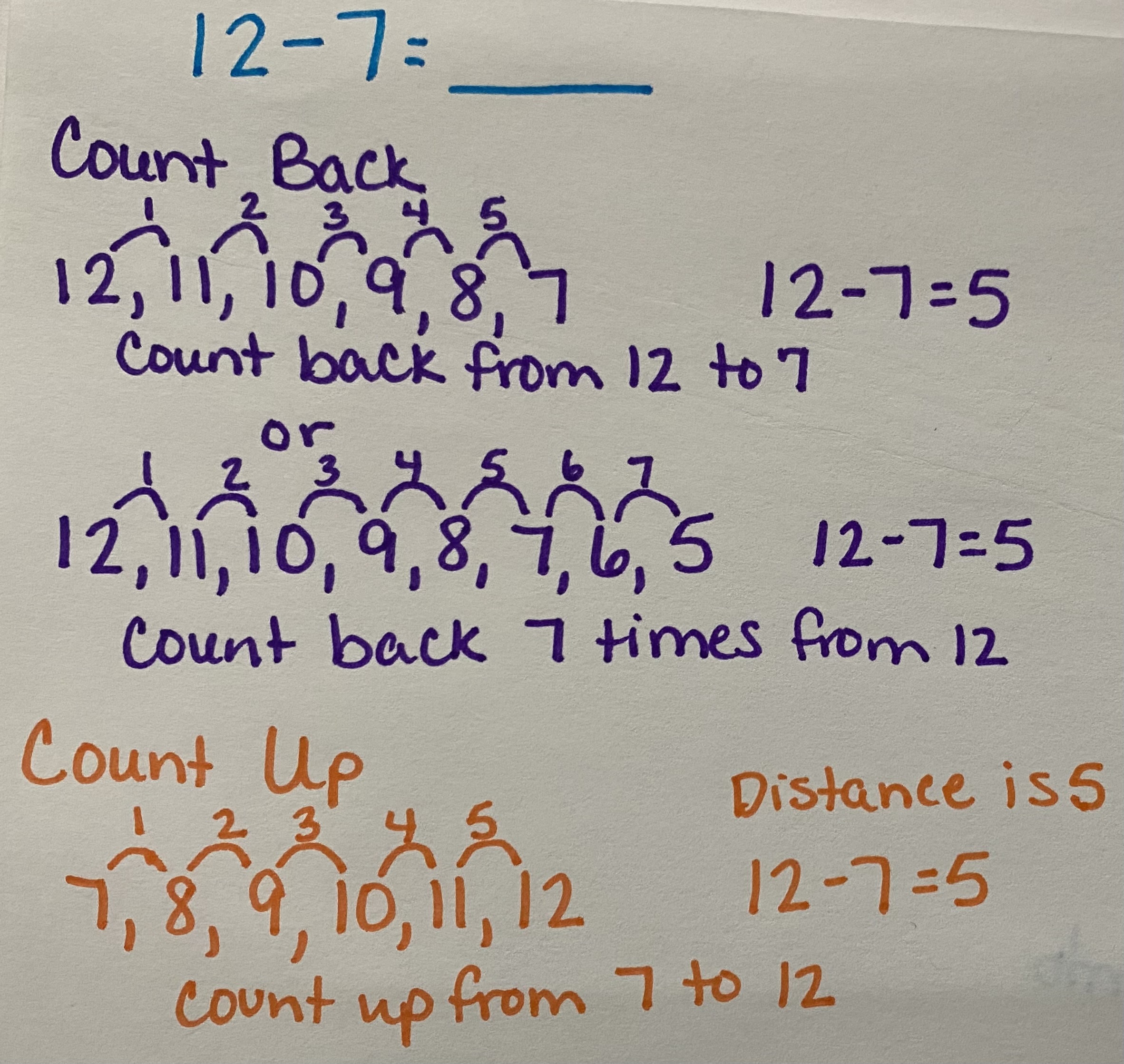
When using the strategy of counting back or even counting up, it is important to remember that subtraction means the difference or distance between the minuend and subtrahend values. When your students understand the relationship of the values and that they can either count back from the minuend or count up from the subtrahend, they deepen their understanding of number sense and how numbers work together. The strategy of counting back or counting up can often be paired with a number line or an open number line as the values worked with increase.
Number Grids
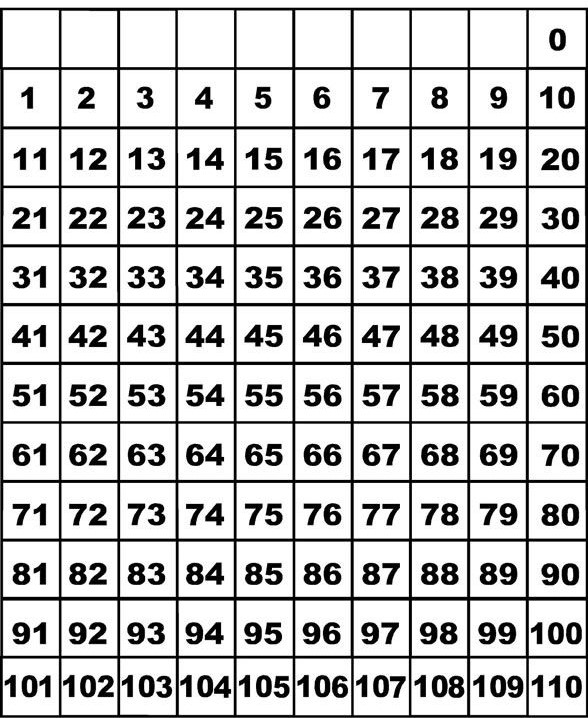
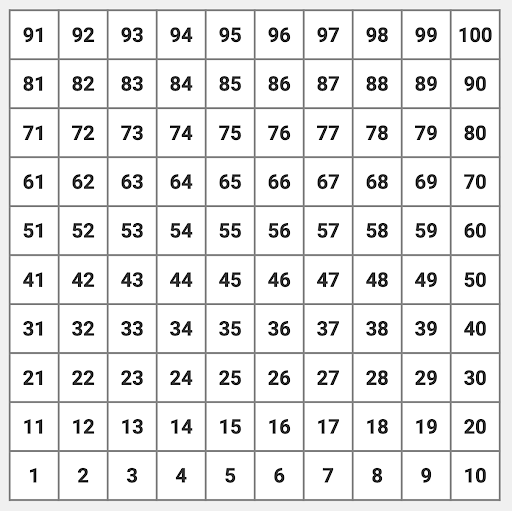
Number grids are a great way for students to look for patterns in subtraction. It begins to build an understanding of place value as students begin looking at what they notice about the tens and ones places. Number grids are uniquely set up in rows of ten to model our base ten number system. As students move across a row, they should notice the digit in the tens place stays the same until the end of the row and the ones place increases by one. As they move up or down a row, they should notice that the ones place stays the same and the digit in the tens place either increases or decreases by one.
Please note the difference in these two number grid. One grid goes from 0 to 110 top to bottom while the other goes from 1 to 100 bottom to top. The one on the left is more commonly used in the classroom, however the one on the right more accurately matched a student's actions of addition or subtraction. As students counts up in addition, the numbers go up the chart. As a student counts back in subtraction, the numbers go down the chart.
Base Ten Blocks
Base ten blocks are a tool utilized many ways in mathematics. In this case, we will be using the base ten blocks representing hundreds, tens, and ones to show the action of subtraction or taking away from one group. Students should start with building representations of the minuend (the number being taken away from), then taking from the minuend, the value of the subtrahend (the number being subtracted), leaving behind the difference. As students learn this strategy, start with numbers where breaking apart groups is not needed. As students become familiar with the action of subtracting, begin the discussions of individual digits in a place value, explore what students think you could do about not having enough in one particular place value. Students can then model making fair trades. As students become more comfortable with the physical manipulatives, move into the visual representation or sketch of the base ten blocks. Teach students that they do not have to draw out individual units, but use "shorthand" sketches of the base ten blocks (a square for the hundreds, a line for the tens, and a dot for the ones). Students can then relate their models to the more abstract standard algorithm for subtraction. This progression of learning is modeled in the video.
Open Number Line
We are all familiar with the number line that young children use. Typically it begins at zero with and counts up by one. An open number line is a blank number line that can be used for any values along the number line that would be useful in solving problems. Typically tick marks are not included on the open number line and as number are added to the number line, they may not be to scale. The open number line is useful in making a representation to record steps of mental computation. Watch the video to see an example of how to use open number lines with subtraction.
Compensation/Give and Take (Constant Differences)
Compensation is a strategy, often carried out in mental math, where one or more numbers is adjusted to make easier-to-use numbers for mental math. For example some value may be taken from or added to either the minuend or subtrahend and then the difference is adjusted to make the problem easier to solve. In the problem 59 - 32, 59 is only one away from 60 and 60 would be easier to subtract from than the 59, and breaking 32 into 30 and 2 will also make mental subtraction easier, giving us the problem 60 - 30 - 2. 60 - 30 = 30, 30 - 2 = 28. Now we need to adjust the problem for the additional one we started with, so 28 - 1 = 27. Another way to solve this same problem using constant differences is to do the same to each the minuend and the subtrahend virtually moving it's location on a number line. Think of the distance between 32 and 59 on a number line, adding one to each value, making the the same distance, now it is the distance between 33 and 60; the problems are equivalent just in a different location on the number line. Building number sense and using the relationship of place values and digits, allows us to deepen our understanding of the operations.
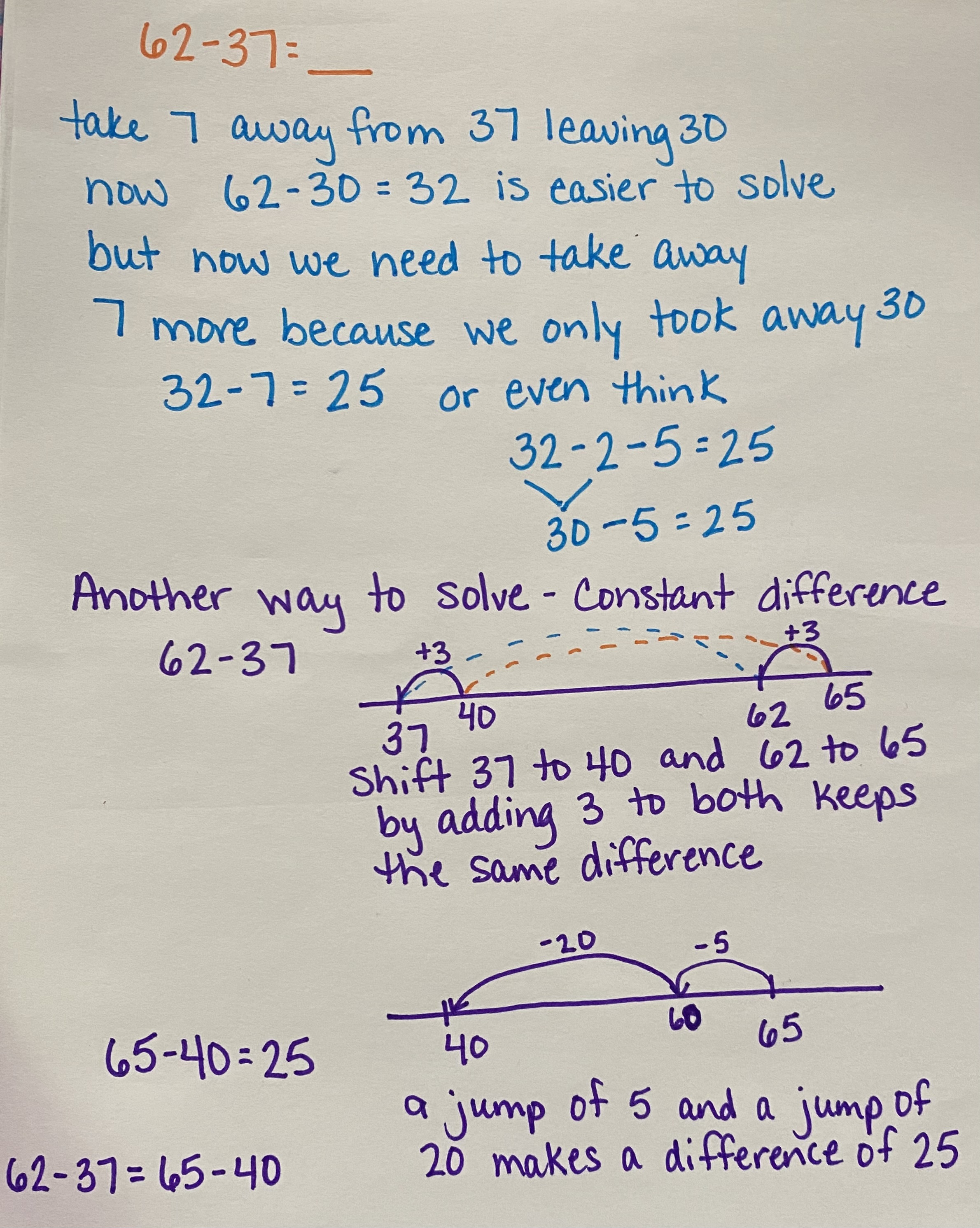
Compensation decomposes (takes apart) or recomposes (puts back together) numbers to make subtraction easier to solve mentally. Students need to understand how numbers can be broken apart and put back together to strengthen their number sense skills.
Expanded Notation (Regroup)
Expanded notation utilizes place value to subtract within each place value, then brings the expanded notation back together to make the final difference. Within expanded notation one place value can be regrouped when necessary to subtract within a place value.
US Standard Algorithm
The US standard algorithm for subtraction is the strategy most adults think of when asked to subtract numbers - stack and subtract. Historically, it is a set of procedures that we were taught in our own schooling. It is an efficient strategy, but it is strictly procedural. When students can utilize more conceptual strategies to build their understanding of subtraction, they then can connect the procedures to that conceptual understanding. Mastery of the standard algorithm is expected by the end of grade 4, however students will be introduced to this strategy much earlier as they are connecting strategies to build deeper knowledge.